【数学】三角形の一部分の面積を求める（三角形の面積/相似）

「面積が10の△ABCの辺BC、CA上に

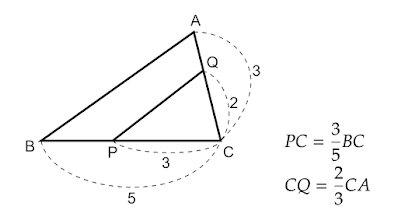
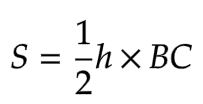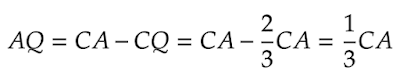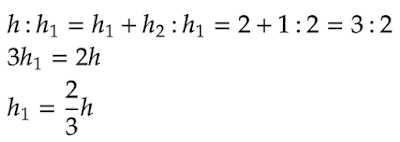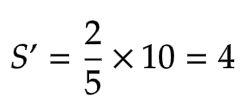 PC = 3/5 * BC, CQ = 2/3 * CA

となるような点P、Qがあるとき△QPCの面積を求めよ。」

というような問題があったとします。問題文だけだと分かりづらいので図で表すと以下のようになります。

この条件で△ABCの一部である△QPCの面積をどのように求めればよいでしょうか？

　まず基本から、三角形の面積は

（底辺）×（高さ）÷2

で知ることができます。なので、△ABCと△QPCにおける底辺と高さそれぞれの関係を調べることで問題を解くことができます。

・底辺の関係

　点Qを考えずに線分APをひき、△ABCと△APCの面積の関係を考えます。

△ABCと△APCは高さが同じで底辺が違うだけです。

このとき、高さをhとして△ABCの面積Sは、（△ABCの面積は10と与えられていますが一時的にSとおきます。）

となります。△APCの面積S1は、

となり、PC = 3/5 * BCの関係と同様にS1 = 3/5 * Sとなりました。

このことから、底辺の比が面積比となることがわかります。

・高さの関係

　次は点Qを含めて△APCと△QPCの高さについて考えます。しかし、高さは与えられていません。

高さと少なからず関係がありそうなのはCA、CQですが、CAとCQの比から高さの関係を導くことはできるでしょうか？

　点Aから辺PCに平行な線を引き、PQの延長線との交点をRとします。

△QPCと△QRAについて考えます。（それぞれの三角形の高さはh1、h2とします。）

CQ = 2/3 * CA より

したがって、CQ : AQ = 2:1　…①

∠PQCと∠RQAは対頂角なので、∠PQC = ∠RQA　…②

PCとRAは平行で錯角の性質より、∠PCQ = ∠RAQ　…③

②、③より、2角が等しいので△QPCと△QRAは相似となります。

相似図形は高さの比も相似比となるため

①より、CQ : AQ = 2:1 = h1 : h2

h = h1 + h2なので、

hは△APCの高さ、h1は△QPCの高さなので、高さの関係はCQ = 2/3 * CAと同様になることがわかりました。また、△APCと△QPCの底辺は同じであるため、高さの比と面積の比が同じであることもわかります。

※後から思ったのですが別解のほうがシンプルでわかりやすいかもしれません。（リンク）

・面積を調べる

　以上のことから△QPCは、△ABCの3/5の底辺で、△ABCの2/3の高さであることがわかりました。

したがって、△QPCの面積をS'とすると、

となります。△ABCの面積Sは問題で10と与えられているので、

となり、問題の答えは4となります。上の性質を理解していれば比の値を面積にかけるだけで簡単に求めることができます。