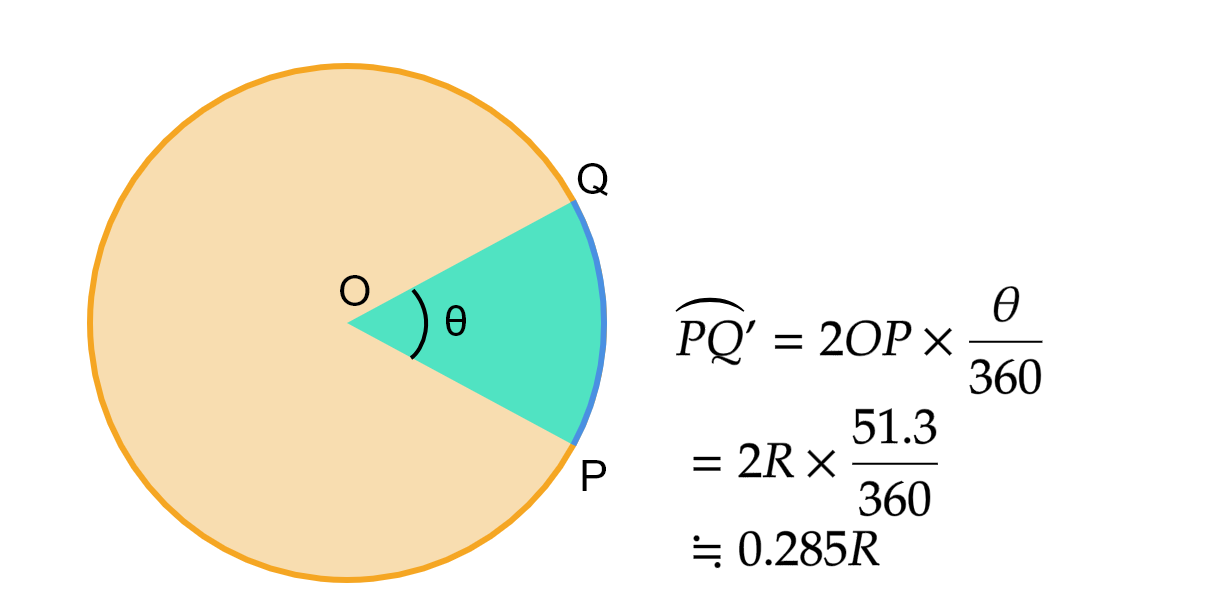地球を球として考えたとき、球面上におけるPQの最短距離を求めよ。半径はRとする。」
球面上の距離で最短距離となりそうなものは2つあります。
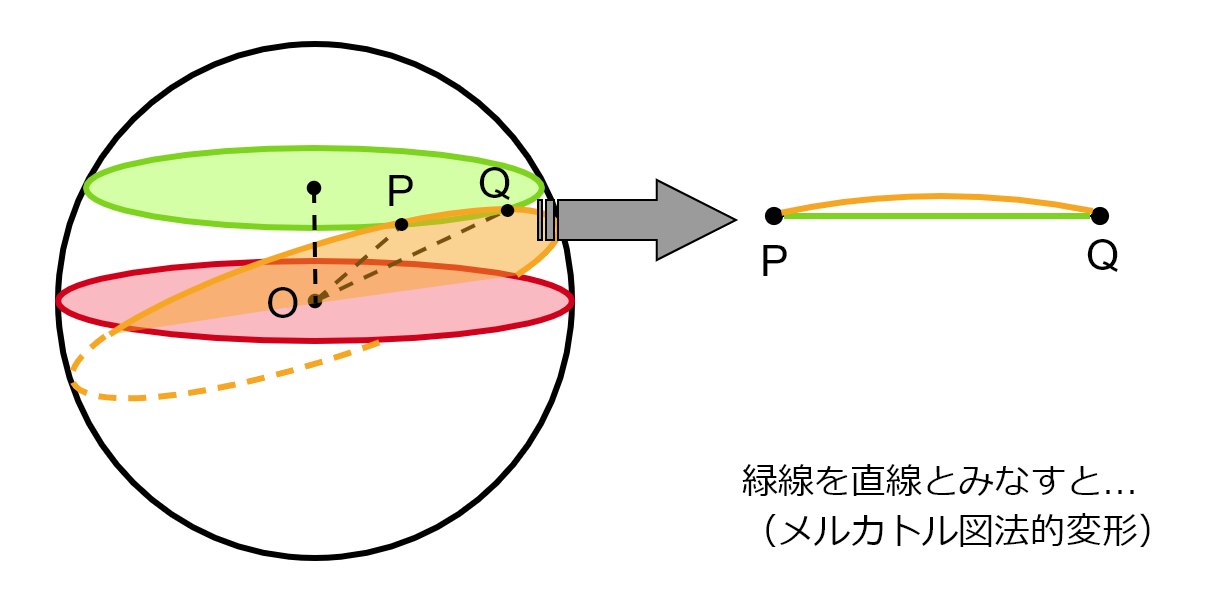
1つは点P、Qがある北緯30°線上を直進するコース（緑線）、もう1つはOP、OQを半径とする円の周上を通るコース（オレンジ線）です。
メルカトル図法のように緯度線と経度線が平面で直交するように変形すると1つ目の緯度線を通る緑線コースは直線に見えるのに対し、2つ目のオレンジコースは北側に曲がっています。
メルカトル図法の地図で起きる誤解のように緑線のほうが最短距離のように思えますが、実際の最短距離はオレンジ線の方になります。
球面上の最短距離は球の中心を通る断面の外周、大円上にあります。
本当にそうなのかを上の問題の条件で緑線とオレンジ線のどちらが短いのかを確かめてみます。
緑線コースの長さ
最初は緑線コースでのPQの長さを求めます。
まず、点P、Qがある30°線によって形作られる円の半径を求めます。
緯度30°ということは、OPは赤道による平面より30°傾いていることになるので、三角比より円O'の半径O'PはRcos30° となります。
PQ間の緑線の長さは扇形O'PQの弧の長さで求められます。
経度差60°ということは中心角は60°、よって弧の長さは円O'の円周の1/6となります。
計算すると弧PQ（＝PQ間の緑線）の長さは0.289R となります。
オレンジ線コースの長さ
次にオレンジ線コースでのPQの長さですが、緯度と経度から計算できません。
なぜなら、オレンジ線は緯度線、経度線のどちらにも平行でも直交しているわけでもないからです。
オレンジ面の赤道面からの傾きはPQの中間地点で最大となるのでOP、OQの傾き30°より大きくなります。
また、扇形O'PQの中心角は60°ですが、大円であるためより半径が長いオレンジ面での扇形OPQは中心角が60°より小さくなります。なので緯度、経度をそのまま使用できません。
なのでまずはPQの直線距離について考えます。
△O'PQに余弦定理をつかって、PQの2乗が求められます。
するとcosθ=5/8 となり、この値からθを求めるとおよそ51.3°となります。
扇形OPQの中心角がわかったので、弧PQ ’（＝PQ間のオレンジ線）の長さを求めると、0.285R となります。
緑線コースの0.289Rよりも短いことがわかります。
球面上の距離が最も短いということは、2地点間の直線距離に最も近い値になるということです。
そして、円の半径が大きくなるほど円周の一部分は見かけ上直線に近くなります。
球体の範囲内で2地点を通るあらゆる円を考えたとき、最も2地点を直線に近い線でつないでいるのは最も大きい半径の円、すなわち大円のときに球面上の距離が最も短くなります。
このことから、オレンジ線コースが最短距離であることがわかります。