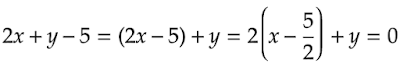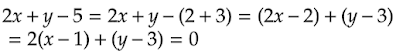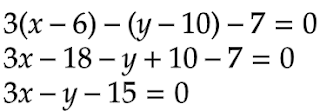①原点(0, 0)から(2.5, 0)へx軸方向に平行移動（赤矢印）
②原点(0, 0)から(0, 5)へy軸方向に平行移動（緑矢印）
③原点(0, 0)から(1, 3)へx軸方向とy軸方向に平行移動（青矢印）
のような方法があります。原点と移動先の点にのみ着目していますが、直線上の点は同様に移動させれば、すべて平行移動後の直線上の点となります。
では、①～③の各方法を軸方向への移動量がわかるようにy=-2x+5 という方程式を変形することはできるでしょうか？
式を変形する
その前に直線の方程式は、ax+by+c=0 という形で表されます。x、y、定数cをすべて左辺に移した形を一般形と呼びます。上記のy=-2x とy=-2x+5 はそれぞれ以下のようになります。
以降直線の方程式は、この一般形で表記します。
①の方法
①の方法はx軸方向に2.5 だけ平行移動しているので、
のように書くと括弧で囲われた部分がx軸方向に2.5（=5/2）だけ移動させていることを表していることがわかります。
また、括弧の部分をXとおけば2X+y=0 となり、元の直線2x+y=0を平行移動したものであるということがわかります。
②の方法
この方法はy軸方向に5だけ平行移動しているので、
と書けます。括弧の部分をYとおけば2x+Y=0 となり、上と同じく元の直線2x+y=0 を平行移動したものであることがわかります。
③の方法
この方法はx軸方向に1、y軸方向に3だけ平行移動しているので、
と書けます。x-1=X, y-3=Y とおけば、2X+Y=0 となり、2x+y=0 を平行移動したものであることがわかります。
これらのことから、元の直線の方程式のxとyにx軸、y軸への移動量を反映させることで平行移動後の直線の方程式を求めることができることがわかります。
確認と公式
「点P(6, 3)を通る3x-y-7=0 に平行な直線の方程式を求めよ。」という問に対して、上記でわかったことを使うと、3x-y-7=0 上の点(0, -7)からP(6, 3)に平行移動すると考えると、x軸方向に6-0=6、y軸方向に3-(-7)=10だけ移動するので、
となります。 …方法A
この式にx=6, y=3 を代入すると、18-3-15=0 となるので、たしかに平行な直線の方程式を求められました。
しかし、直線の平行移動には公式があり、上の問いのように(p, q)を通るax+by+c=0 に平行な直線の方程式は、
で表されます。
これを用いて、a=3, b=-1、点Pの座標からp=6, q=3 なので
と、求めることができます。 …方法B
なぜ異なる方法で、同じ結果が出るのかを考えます。
なぜ同じ結果になるのか？
まず、方法Aのやり方で考えます。
原点を通る直線の方程式ax+by=0 を平行移動してax+by+c=0 になるとします。このとき、ax+by=0 上の原点(0, 0)がax+by+c=0 上の点(m, n)に移動するとします。
移動量はx軸方向にm、y軸方向にnとなるので、
となります。これはax+by+c=0 と同じ直線を表しているので、c=-am-bn であることがわかります。
次に、この直線ax+by+c=0に平行で点（p, q）を通る直線を考えます。
ax+by+c=0 上の点(m, n)が(p, q)に移動するので、その移動量はx軸方向にp-m、y軸方向にq-n となります。
したがって、
となります。前述の通りc=-am-bn であるので、展開して出てきたam+bn を消して-ap-bqだけが定数部分として残ります。そして、
と変形できることから、「ax+by+c=0 に平行で点(p, q)を通る直線」を考えるときは、「原点を通り傾きが同じである直線ax+by=0 に平行で(p, q)を通る直線」に置き換えて考えることができ、置き換えた式が方法Bの直線の平行移動の公式となっていることがわかります。
 |
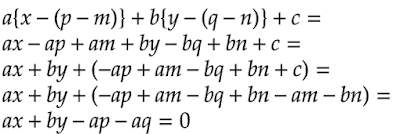| ※最後の行 [誤]-aq [正]-bq |
なので、方法Aと方法Bは同じ結果になります。