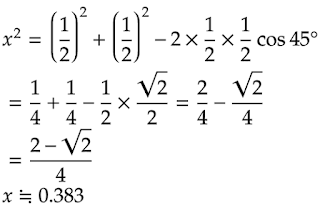なので直径を1とすると、円周は3.14となるわけです。
正六角形の場合
まずは六角形から始めます。
直径が1の円に内接する正六角形があります。直径1の円の円周はπ≒3.14です。円の中心を通る対角線を引くと正六角形は6つの三角形に分割されます。
対角線は直径でもあり、中心で6つ、つまり60°ごとに分割されているので、分割された三角形を1つ取り出すと、長さ0.5(=1/2)の辺が2つあり、その2辺の間の角は60°です。
頂角が60°の二等辺三角形、つまり正三角形であることがわかります。
頂角が60°の二等辺三角形が正三角形であることの証明
このことから赤線の長さも0.5なので、正六角形の周の長さは
0.5×6 = 3
となります。直径は1なので直径に対する周の長さの割合も3です。
円周は正六角形の周の長さより長いので、3よりも大きいのですが、円周率の近似の1つとして利用することができます。
ざっくり円周を計算したいときは直径の3倍とすれば、大まかな長さを求めることができます。
正八角形の場合
次にタイトルの通り八角形の場合を考えます。
正六角形の時と同様直径1の円に内接する正八角形を考え、円の中心を通る対角線を引きます。
中心を通る対角線は4本引けるので、正八角形は8つに分割されます。
その一つを取り出すと、2辺の長さが0.5で、頂角が45°の二等辺三角形となっています。
よって正八角形の周の長さは、
0.383×8 ≒ 3.06
となり、正六角形のときよりさらに3.14に近づきました。
このように頂点の多い多角形は円に近い形になるのでより正確に円周率を求める事ができるようになります。
関連記事:円に内接・外接する正多角形の周の長さを求める公式を作ってみよう(ブログ:数学について考えてみる)