|
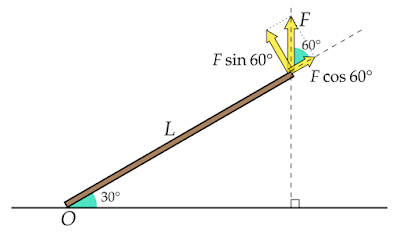
| 図1 力のモーメント |
「床の上に長さLの棒がある。棒のO端が支点となるように他端を鉛直上方向に力Fを加え、図1のような状態になった。
このときO端まわりの力Fによる力のモーメントはいくらになるか。棒の太さは考慮しないものとする。」という問題について考えます。
棒に垂直な力の大きさはFsin60°になるので、力FによるO端まわりの力のモーメントはFLsin60°となります。この方法を解法Aとします。
実際、Oから棒と平行な方向を持ち大きさLのベクトルを考えた時、鉛直方向に床面に棒を投影(正射影)したときの長さはLcos30°となります。したがって、力FによるO端まわりの力のモーメントはFLcos30°となります。cos30°=sin60°なので、先ほどの答えと同じになります。この方法を解法Bとします。
それを知るために、次は上記の問題の力Fが反時計回りに60°傾いていた場合の力のモーメントを考えてみます。
解法A
 |
| 図5 力Fの分解2 |
解法B
 |
| 図6 力Fの分解と床面に棒を投影 |
正射影した棒の長さは先ほどと同じLcos30°ですが、力の向きが鉛直上向きではないので力Fの鉛直成分を求めます。力Fは鉛直方向から60°回転しているので、鉛直成分はFcos60°となります。
したがって、力FによるO端まわりの力のモーメントはFLcos30°cos60°となるのですが、先ほどと答えが違います。cos60°がついているためより小さくなってしまっています。
力のモーメントとは、ある点(記事中ではO端)と作用線(記事中では力の始点を通り、力と平行な線)の距離と力の大きさの積で表されます。
 |
| 図7 必要な成分をすべて書き出す |
ここで先ほどの問題点に戻ります。力Fを成分分解しましたが、まだ力Fの水平成分Fsin60°が出てきていません。そしてその力Fの水平成分Fsin60°の作用線とO端との距離は、ちょうど床に垂直な壁に棒を投影したときの正射影の長さLsin30°に等しいです。この2つから求められる力のモーメントを考えていなかったことが、計算が合わない原因です。
一方で解法Aがシンプルなのは、力FをO端を通る作用線とそれに直交する作用線方向に分解しているからです。前者は距離が0になるので力のモーメントの大きさも0になり、後者の力のモーメントのみを考えれば良いのです。
 |
| 図8 力のモーメントの定義に従った解法 |
図8のように線を引くことで力Fの作用線とO端の距離はLcos30°であることが求められます。したがって、力FによるO端まわりの力のモーメントはFLcos30°と求めることができます。
このように、力Fの作用線とO端の距離を求めることができれば、シンプルに力のモーメントの大きさを計算することができます。