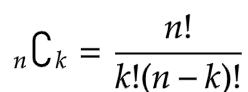|
| パスカルの三角形 |
上の画像の左がパスカルの三角形です。aあるいはbの次数順に並べた時、対応した段の数字の順番で各項の係数が並びます。
それは画像右のようにn=1 を最上段として下へn=2、n=3…のときの係数を並べているからです。
そして、ある項の係数はパスカルの三角形の右上と左上の数の和になるという性質があります。
3段目左から2番目の「3」は左上の「1」と右上の「2」の和になりますし、
5段目右から3番目の「10」は左上の「6」と右上の「4」の和になります。
たとえ何乗のどの項の係数でも、組み合わせの計算を知らなくても、パスカルの三角形を下へ下へと計算しながら書いていけば求めることができます。
では、本当に何乗の二項の展開式でもこの三角形から係数を求められるのでしょうか?
パスカルの三角形のn-1乗の段とn乗の段について考えます。
 |
| (a)nとn-1の段から係数の関係式を組み立てる |
n乗の段のk番目はn-1乗の段の左上と右上つまりk-1番目とk番目の和になります。(a)の矢印の式です。
このとき、n:自然数、k:1≦k≦nを満たす自然数 です。
また、C(組み合わせ)は階乗で表すことができるので、(a)の下の式に変換します。
 |
| (b)(a)の右辺の計算 |
右辺の分数式を計算すると、(b)の1行目のように(n-1)!をくくりだして{}部分ができます。
| (c)階乗の変形 |
すると、(b)の2行目になり約分、(c)を利用して左辺と同じものを導くことができました。
このことから、(a)にある式、すなわちパスカルの三角形の和の性質は成り立つため、たとえ何乗の係数でも求めることは可能であることがわかりました。